3.2. Cardinal arithmetic

An algebra of functions

For this section, suppose that $f:A\to B$ and $g:B\to C$ are functions.

Definition (Composition).

The composition of $f$ and $g$ is the function $g\circ f:A\to C$ given by $g\circ f(a):=g(f(a))$.

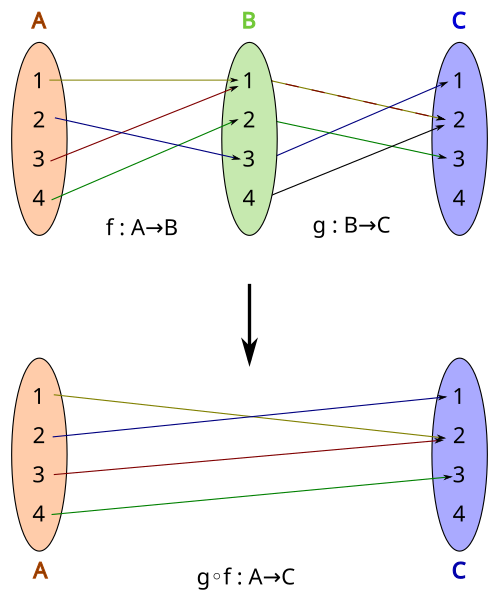
Exercises.

1. Prove that the composition of injective (surjective) functions is again injective (surjective).

2. Assume that $g\circ f$ is injective (surjective). What can you say about the injectivity (surjectivity) of $f$ and $g$?

If $f$ is bijective, the inverse of $f$ is the function $f^{-1}=\{(b,a):(a,b)\in f\}$ from $B$ to $A$. Why is bijectivity, that is the fact that $f$ be both injective and surjective, important here?

Definition (Restriction).

The restriction of $f$ to $D\subseteq A$ is the function $f{|}_D:D\to B$ defined by $f{|}_D(x)=f(x)$.

Examples.

1. The restriction of a constant function is constant.
2. The restriction of an injective function is injective.
3. The restriction of the identity on a set $X$ to any subset of $X$ is the identity on that subset.

Notation.

The set of all functions $A\to B$ is denoted by $B^A$. This choice of symbol is motivated in the tutorials, where it is shown that for finite sets $|B^A|=|B{|}^{|A|}$.

Equinumerosity

Note:

This topic is introduced in the lectures. The discussion is inadequate for these notes.

To measure is to compare.

Notation.

I abbreviate the phrase “there exists a bijective function $X\to Y$” by writing $|X|=|Y|$. I will also say $X$ and $Y$ are equinumerous, or have the same size.

This symbol has the following properties, which you should verify yourself.

Proposition.

For any set $X$,

1. $|X|=|X|$ (Reflexivity).
2. If $|X|=|Y|$, then $|Y|=|X|$ (Symmetry).
3. If $|X|=|Y|$ and $|Y|=|Z|$, then $|X|=|Z|$ (Transitivity).

Compare these properties with others mentioned in previous chapters, such as here.

Metamathematical warning (safe to ignore):

Despite appearances, it is not correct to say that this symbol defines an equivalence relation. An explanation for this goes well beyond the scope of this course but will be mentioned in the lectures.

For the sake of intuition, you can think of cardinal numbers as precisely the equivalence classes of this relation.

Finite sets revisited

Earlier I defined the word finite in terms of natural numbers. Indeed, a way to rewrite my earlier definition is that a set $X$ is finite if there is a natural $n$ such that $|X|=|\{0,\dots ,n-1\}|$. In this case, it is shorter to just write $|X|=n$, but I must first convince you that this is well-defined.

Reflect.

Well-defined, in this instance, means that there could be more than one natural satisfying the definition. How do you know which one to pick? Of course this does not happen, but I must prove this to you.

It wasn’t until 1888 that Dedekind came up with a definition of finite set that did not need the naturals to be constructed first. I will not use the definition, but if you are curious, one can prove that a set is finite if and only if it is not equinumerous with a proper subset of itself. This can be used to define finiteness without reference to any numbers. The fact that $\mathbb{N}$ is infinite in this context is known as Galileo’s paradox.

A subset $A$ of a set $B$ is called a proper subset, denoted $A⊊B$ if $A\subseteq B$ but $A\ne B$.

Lemma.

For every natural $n$, there is no bijection from $\{0,\dots ,n\}$ to a proper subset of it.

Proof:

Removed during Quiz 5.

Corollary.

1. If $n$ and $m$ are two naturals witnessing the finiteness of the same set $X$, then $n=m$.
2. $\mathbb{N}$ is infinite.

This really is the classic children’s game “my number is your number plus one.”

Proof of 2:

By contradiction, suppose that $f:\mathbb{N}\to \{0,\dots ,n\}$ is a bijection. Obviously $n>0$; then the function $f{|}_{\{0,\dots ,n\}}$ is a bijection onto its image. The number $f(n+1)$ belongs to the domain but not the image and thus $f$ contradicts the lemma.

Exercise.

Prove that the set of prime numbers is an infinite subset of $\mathbb{Z}$.

Hint.

Let $F$ be a finite collection of primes, then notice that $n:=\prod F$ and $n+1$ are relative primes. Conclude using FTA that no finite set of primes contains all primes.

I can finally formalize the idea that finite plus finite is finite:

Theorem.

The union of finite sets is finite.

Other than the union, what other operations on sets preserve finiteness?

Theorem.

The powerset of a finite set $X$ is finite. Moreover, it has size $2^{|X|}$.

Proofs in tutorials.

Hard exercise.

Prove from the definition that a subset of a finite set is finite.